中科院南京土壤所满俊课题组ACS ES&T Engg.:波动地下水位下的蒸气入侵场地表征——一种机器学习增强的集成平滑框架
- 2026-02-13 20:52:36
英文原题:Vapor Intrusion Site Characterization under Fluctuating Groundwater Tables: A Machine Learning-Enhanced Ensemble Smoother Framework

通讯作者:满俊,中国科学院南京土壤研究所
作者:Ruobing Wu, Lei Ju, Yun Liu, Jun Man
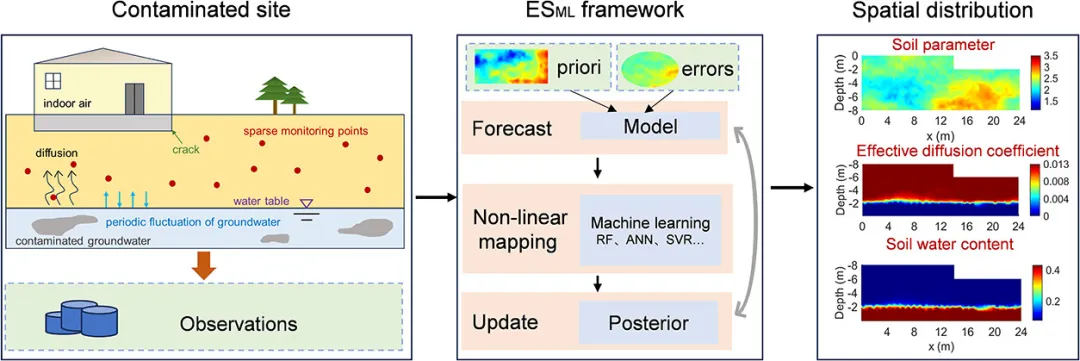
近日,中国科学院南京土壤研究所满俊副研究员小组提出了一种机器学习增强的集成平滑框架(ESML),以应对地下水位波动对蒸气入侵(VI)场地表征带来的挑战。该框架能够有效融合多源数据,实现对VI风险的快速、准确评估,并为污染场地的监测和管理提供新思路。
挥发性有机化合物(VOCs)通过蒸气入侵(VI)对室内空气构成严重健康风险。可靠的VI评估关键在于准确刻画控制水分运移的非均质土壤水力特性。然而,当前模型普遍存在两大缺陷:一是过度简化土壤非均质性;二是常忽视普遍存在的地下水位(GWT)波动这一动态水文驱动因素。这种波动会显著改变包气带污染物分布,致使室内VOCs浓度激增,在受潮汐影响的沿海填海区尤为突出。面对高维参数反演困境,传统的集合平滑器(ES)等数据同化(DA)技术很少能同时应对动态GWT波动与极端数据稀缺的挑战。近期虽出现了机器学习增强的DA框架,但仍受主观模型选择、计算成本高等限制,且未系统探究波动幅度与周期对参数可识别性的影响。
针对上述问题,中国科学院南京土壤研究所满俊副研究员小组提出了一种基于机器学习增强的集合平滑框架,该架构通过集成机器学习(包括随机森林(RF)、人工神经网络(ANN)和支持向量回归(SVR))学习的非参数更新算子取代了传统ES更新,以实现精准的土壤水力特性表征。该工作为在数据有限且水文状况多变的地区进行表征提供了一条经济高效的途径。
在虚拟案例中,我们模拟地下水位波动(振幅A=2米,周期T=4天)条件,分别采用ESRF、ESANN与ESSVR三种机器学习增强集成平滑方法,反演获得土壤关键水力参数ln(α)场的均值与方差估计(图1)。整体上,三种ESML方法均能重建参考场的主要空间分布特征(图1a),成功识别出参数低值区(x=2–12米,z=-7–-4米)与高值区(x=12–22米,z=-8–-4米)(图1b,d,f)。此外,ESML还成功捕捉到土壤含水量的动态变化(图2)及其对应有效扩散系数的变化(图3)。具体而言,在地下水位高峰时(第21天;图2a),毛细边缘区延伸抑制了水位以下区域的土壤气迁移(图3a);水位下降阶段(第22天;图2b),水分再分配扩大非饱和区,促使气相扩散系数快速上升(图3b);地下水位最低时(第23天;图2c),非饱和区厚度最大,扩散系数达到峰值(图3c)。可以发现,ESRF均值估计场与参考场较为相似(图1a和1b),并且不确定性较小(图1c)。三种方法ESRF、ESANN与ESSVR的相应RMSE值分别为0.30、0.35和0.45。以上结果表明,ESRF比另外两种方法在反演中表现更为突出,被选定为后续分析的核心算法。
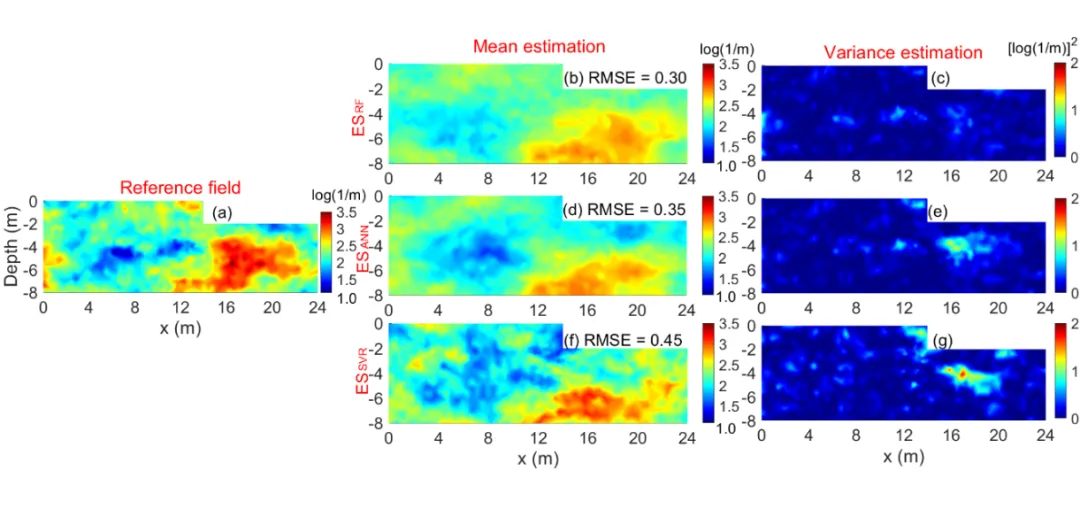
图1.(a)参考ln(α)值以及通过ESML得到的平均估计值(b,d,f)和方差估计值(c,e,g)
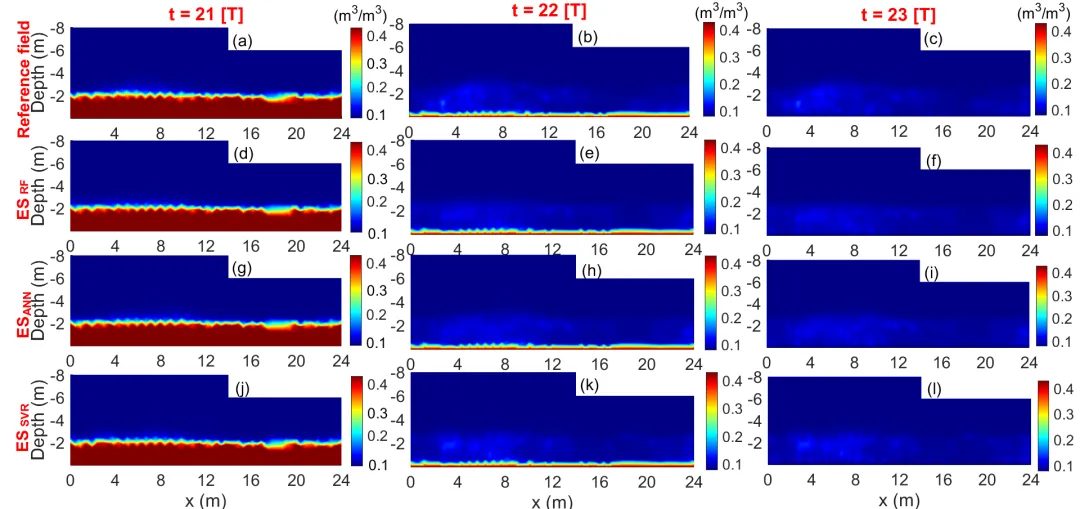
图2.土壤含水量的时空分布情况。(a-c)21-23日的参考分布情况,以及由ESRF(d-f)、ESANN(g-i)和ESSVR(j-l)估算的相应分布情况
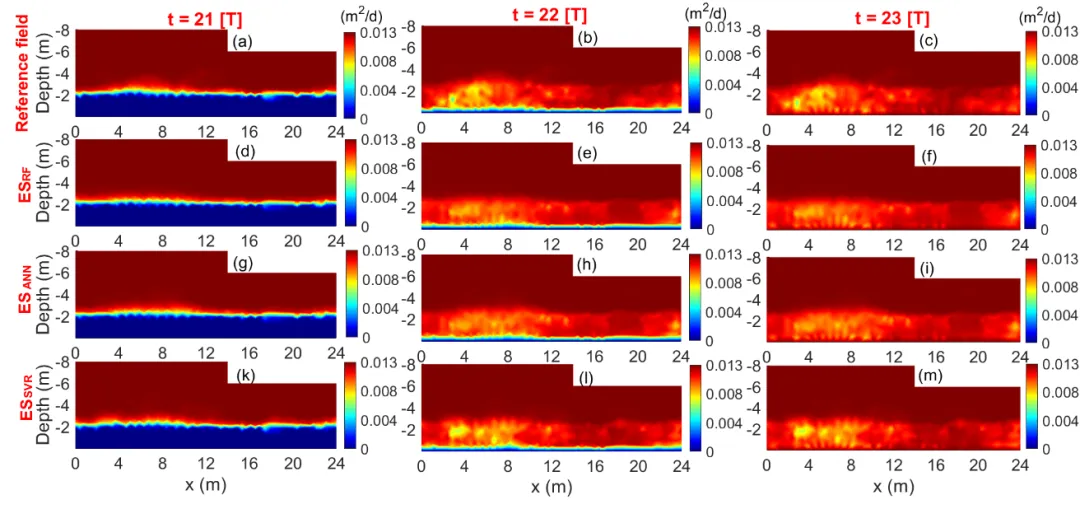
图3.有效扩散系数的时空分布情况。(a-c)21-23日的参考分布情况,以及由ESRF(d-f)、ESANN(g-i)和ESSVR(j-l)估算的相应分布情况
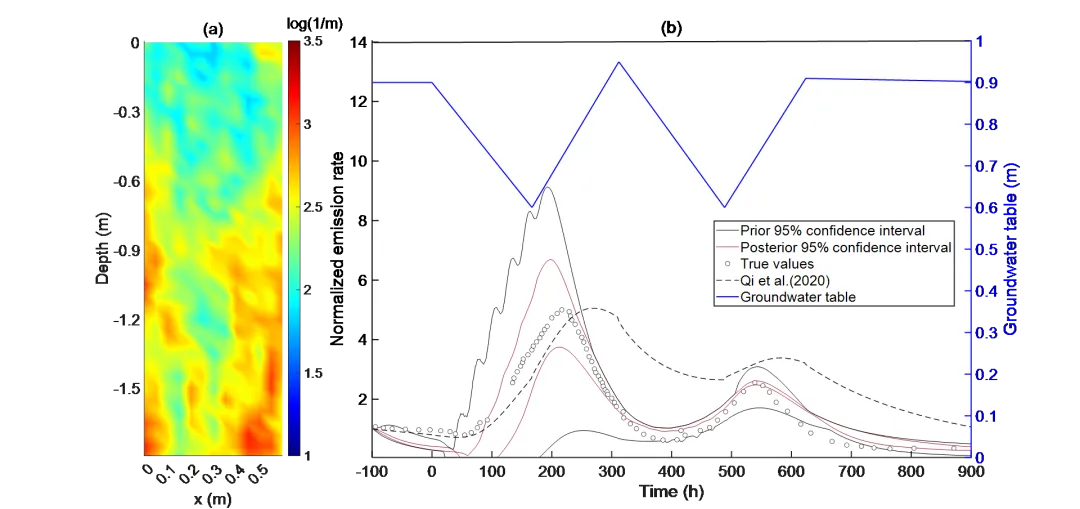
图4.(a)实验室沙箱实验中ln(α)场的平均估计值,(b)地下水位、先验95%置信区间以及基于ESRF的后验95%置信区间以及标准化TCE排放速率的测量值
图4通过评估实验室砂箱实验进一步评估了ESRF。ESRF成功反演了土壤水力参数场(图4a),并预测了TCE排放通量(图4b)。相比均质土壤假设(黑色虚线)的模拟,ESRF预测与实测结果具有更高的一致性(R²=0.91),且排放通量与地下水位呈现预期的负相关趋势。虽然在排放峰值存在微小偏差(在±30%以内),但后验置信区间完全覆盖两个完整波动周期内的测量轨迹,且较先验区间显著收窄,表明观测有效降低了参数与预测的不确定性。结果证实,ESML框架能实现动态条件下对蒸气入侵过程的可靠表征,适用于长期风险评估。
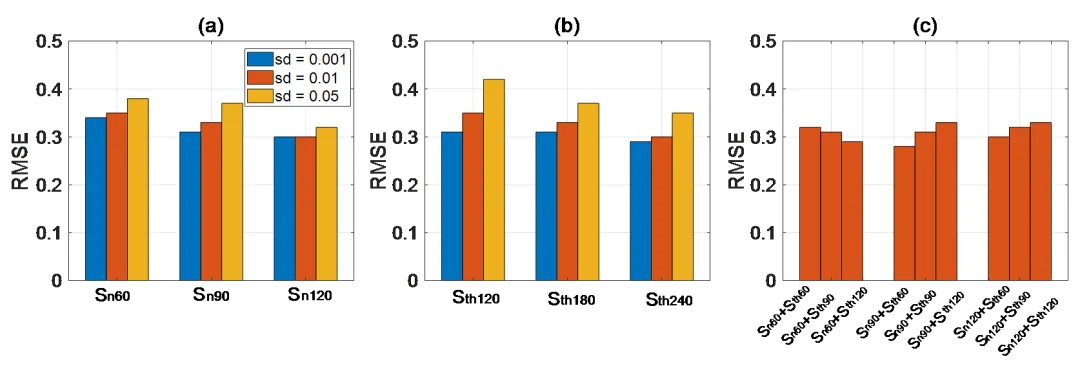
图5.通过融合(a)土壤气浓度、(b)土壤含水量以及(c)他们的组合所计算出的RMSE值
图5评估了不同观测类型、数量和误差水平下的反演性能。无论是土壤气浓度还是含水量数据,观测数量与RMSE均呈稳定负相关。值得注意的是,在σ≤0.01条件下,增加土壤含水量观测可获得与土壤气浓度观测相当的精度。研究发现,联合同化相比单一数据类型可提升性能(图5c),但其效果严重依赖于数据特征。当气体数据较少时,(Sn60),加入含水量观测可有效降低RMSE(0.32→0.29),表明两类信息具有互补性。然而当土壤气浓度数据充足时(Sn90/Sn120),继续增加含水量观测会因信息冗余、噪声放大而降低精度(如Sn90条件下RMSE从0.28升至0.33)。
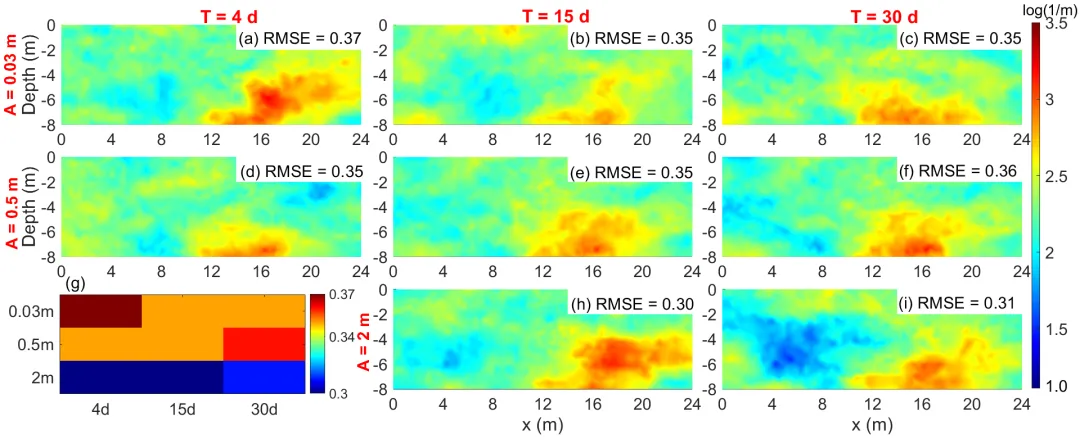
图6.通过整合不同土壤水汽浓度数据,得到在不同土壤水位波动周期和幅度下估算的ln(α)值。这些情景按照土壤水分波动幅度进行分组:(a-c)A=0.03米,(d-f)A=0.5米,(h-i)A=2米。在每个幅度组内,分别针对T=4天、15天和30天的周期进行结果分析。(g)所有测试情景下对应的相关RMSE值的汇总
图6表明,在不同地下水位(GWT)波动情景下,ESML方法均能捕捉到参考场的关键空间分布。反演RMSE始终在0.30至0.37之间。误差分析显示,波动幅度是影响精度的主导因素:振幅2米时的RMSE(0.30–0.31)显著低于0.03米(0.35–0.37)与0.5米(0.35–0.36)的情景,对波动的敏感度(平均绝对梯度0.77)远高于对周期(0.19),周期变化对精度影响甚微。进一步对比观测信息量(图7)发现,同化气体浓度获得的熵值(12–18)远高于同化土壤含水量熵值(3–7),前者在反演中提供更强的约束。在所有情景下,信息增益与RMSE均呈现显著负相关(p<0.05),表明更高的信息量通常对应更高的反演精度。
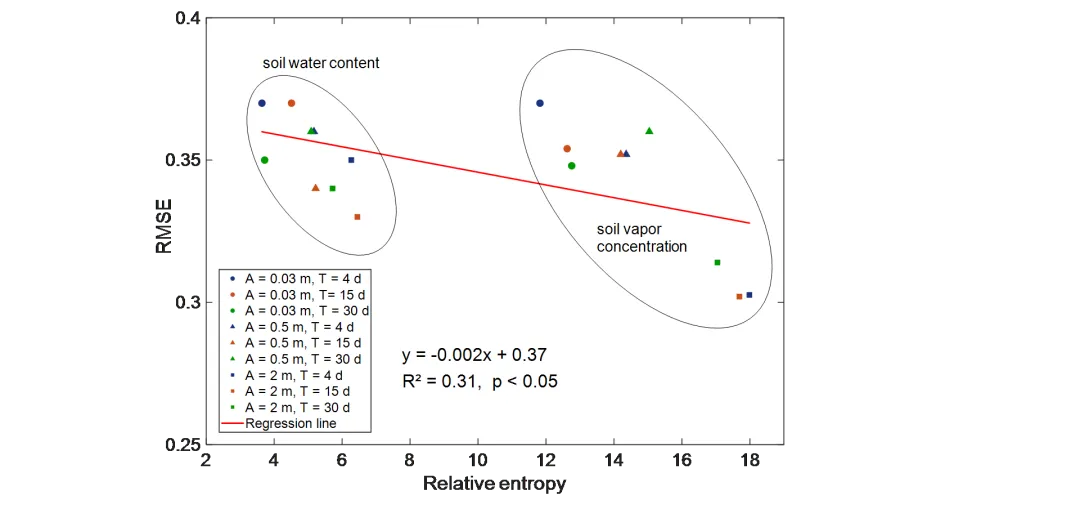
图7.不同GWT波动情景下反演结果的RMSE与相对熵值之间的关系图
综上所述,对于虚拟场地和砂箱实验,ESML方法有效实现了动态水文条件下空间异质的土壤水力参数估计。研究表明,地下水位波动幅度是参数可识别性的主要控制因素,而波动周期影响甚微。同时特定观测误差下,土壤含水量数据可替代土壤气浓度数据。该框架为动态水文驱动的场地风险评价提供了经济有效的工具,未来可扩展至优先路径等复杂情形。
相关论文发表在ACS ES&T Engineering上,南京师范大学与中国科学院南京土壤研究所联合培养的硕士生吴渃冰为文章的第一作者,中国科学院南京土壤研究所满俊副研究员为通讯作者。


往期推荐



扫描二维码,快速入群~
